| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 모두의 딥러닝
- Deep_Learning
- 인공지능
- DeepLearning개념
- DataSet
- neuralnetwork
- Artificial Intelligence
- suninatas
- TrainingDataSet
- sql_injection
- HiddenLayer
- tensorflow
- FC layer
- 모두의딥러닝
- Neural Net
- relu
- 머신러닝
- digitalforensic
- ai
- labelImg
- Model Ensemble
- blindsqlinjection
- 딥러닝
- forensic
- Learning_Rate
- 텐서플로우
- Softmax Classification
- LogisticRegression
- NeuralNet
- TestDataSet
- Today
- Total
InformationSecurity-Study
[모두의 딥러닝] Convolutional Neural Networks 본문
1단계: ConvNet의 Conv 레이어 만들기
고양이에게 어떠한 형태의 그림을 보여주었을 때, 그림을 읽어들이는 뉴런이 모두 동작하는 게 아니라 그림의 형태에 따라서 일부분 일부분만 사용하는 것을 알 수 있다.
이 발견에서 착안한 것이 Convolutional Neural Networks라고 한다.

(CONV - RELU - POOL)의 과정을 여러 번 반복해서 레이블링하는 Softmax Classification을 통해 분류한다.

처음의 Input 32x32x3 Image --> 5x5x3 filter (한꺼번에 얼마만큼 보고 싶은지 정한다. )
filter는 궁극적으로 한 값(one number)을 만들어낸다. one number에 대한 공식이 아래와 같다.
one number = Wx + b = RELU(Wx+b)

똑같은 필터로 이미지의 다른 부분도 봐야하기 때문에 옆으로 넘기면서 각각의 값(one number)들을 가져온다.
같은 weight을 가지고 전체를 훑은 다음에 각각의 number들을 가져온다.
몇개의 점을 가져올 수 있을까? 이 값들을 알아야 weight을 정할 수 있기 때문이다.
ex) 7x7 input (spatially) assume 3x3 filter
==> 5x5 output (stride:1 한 칸씩 옆으로 움직일 경우)
==> 3x3 output (Stride:2 두 칸씩 옆으로 움직일 경우)
==> NxN input --> Output size: (N-F)/Stride+1

그림이 급격하게 작아지는 것을 방지하고 모서리임을 네트워크에 알려주기 위함이다.
원래 Input 7x7 Image --> 3x3 filter, applied with stride 1 (3x3 filter 크기의, 1칸씩 옮겨가면서 본다)
pad with 1 pixel border = > 9x9 input 으로 늘어난다.
그 다음 똑같은 공식을 이용해서 적용하면 된다. (9-3) / 1 + 1 = 7
즉, Convolutional layer을 해도 input과 output의 사이즈가 같다. ==> 특 장점!
다른 set에 weight이 있으니 filter1에서 온 이미지에 filter2를 만드는 방법이 있을수도 있.
filter는 각각 weight이 다르기 때문에 여러 개의 filter을 적용하면 acitvation maps(이미지 사이즈,이미지 사이즈,filter의 개수
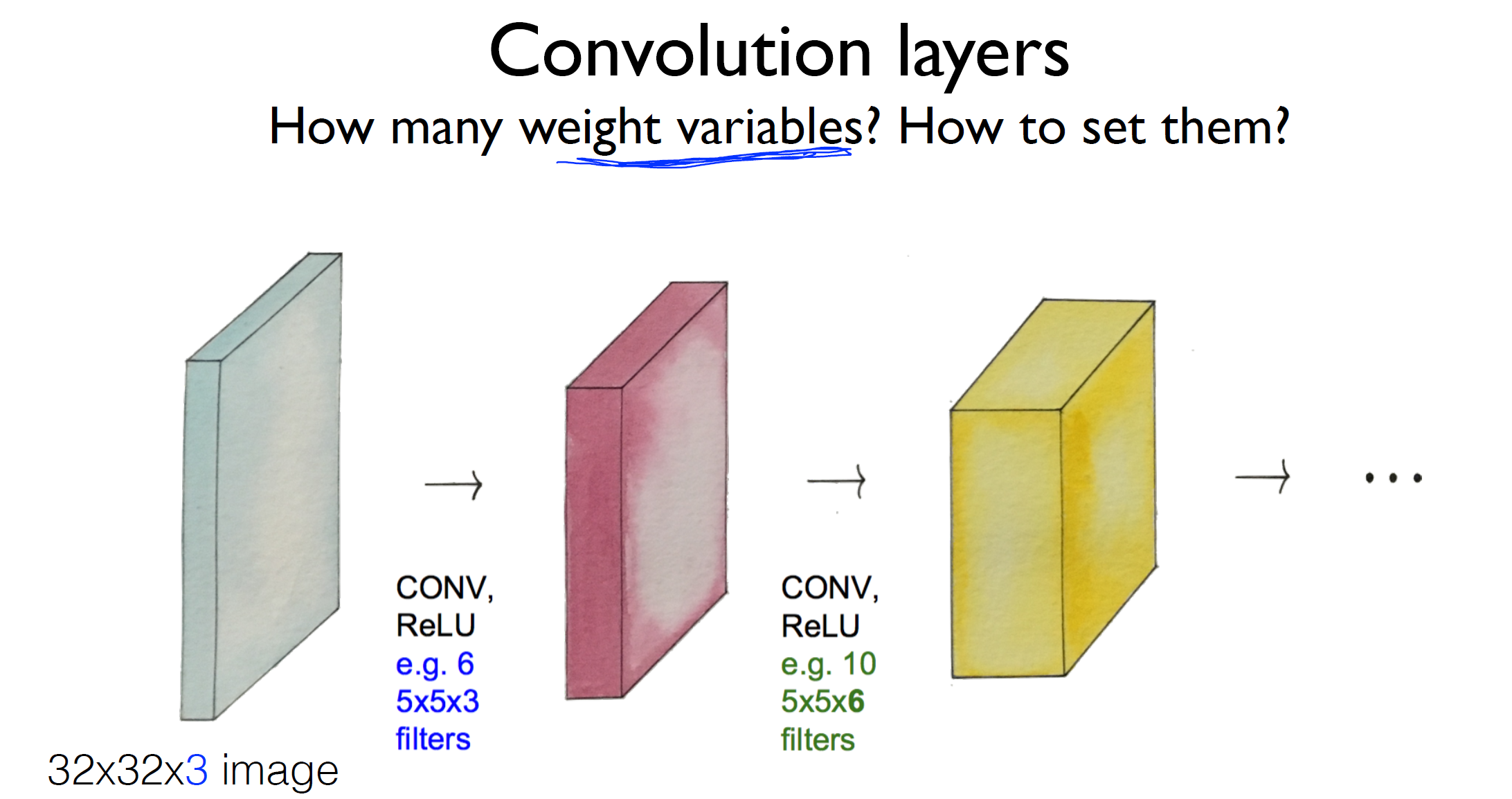
Convolution layer
32x32x3 image -> 5x5x3 filter -> 26x26x3 image -> 5x5x6 filter -> 21x21x3 image -> ...
짚고 넘어가야할 것은 weight에 사용되는 variable의 개수는 어떻게 될까?
여기서 weight의 개수는 첫 filter에 6개를, 두번째 filter에 10개를 쓰는 것을 볼 수 있다.
처음에는 random하게 initialize하지만 가지고 있는 데이터로 학습을 하게 되는 것이다.
2단계: Max pooling and others

CONV - RELU - POOL의 반복을 통해서 Softmax Classification 하는 것을 위에서 확인하였다.
이때 Pooling layer란 간단하게 sampling이라고 생각하면 된다.
한 layer에서 이미지를 가지고 resize하면 사이즈가 작아지는데, 이 사이즈를 작게 만드는 것을 말한다.
2x2 size의 filter, stride 2 --> 2x2 output (= (N-F)/stride + 1 )
4개의 박스가 나오는데, 여기서 MAX POOLING은 각각의 박스에서 가장 큰 값을 뽑아내는 것이다.
그래서 2x2 output에는 {6, 8, 3, 4}의 값을 갖는다.
Fully Connected Layer (FC layer)
POOLING 샘플링의 횟수는 원하는 대로. 보통 마지막에 한 번 더 풀링한 다음에 Softmax Classification을 거친다.
이 부분은 앞에서 충분히 이야기를 많이 하였기에 쉽게 이해할 수 있으리라 믿는다.
거의 끝이 보이는 것 같다. 조금만 더 힘을 내자.
'인공지능' 카테고리의 다른 글
| Tensorflow Object Detection API train own data 1단계 (0) | 2019.05.15 |
|---|---|
| [모두의 딥러닝] 딥러닝을 잘하는 방법: dropout & model ensemble (0) | 2019.05.04 |
| [모두의 딥러닝] 딥러닝을 잘하는 방법: 초기값 설정! (0) | 2019.05.04 |
| [모두의 딥러닝] Sigmoid 보다 ReLU가 더 좋다 (ReLU가 뭐길래??) (0) | 2019.05.04 |
| [모두의 딥러닝] Tensor Board로 딥 네트워크 들여다보기 LAB02 (0) | 2019.05.02 |
